Section2:学習率最適化手法

勾配降下法の復習

・学習率が大きすぎると発散してしまう ・学習率が小さすぎると、極端に遅くなる＆大域局所最適値に収束しづらくなる

初期の学習率の設定方法の指針は以下の2つ

・初期の学習率を大きく設定し、徐々に学習率を小さくする。 ・パラメータごとに学習率を可変させる。

学習率の最適化は、学習率最適化手法を利用。

■各手法について

1.モメンタム

勾配降下法では、誤差をパラメータで微分したものと学習率の積を減算していました。 モメンタムでは、誤差をパラメータで微分したものと学習率の積を減算した後、現在の重みに前回の重みを減算した値と慣性の積を加算する。

$V_t=μV_{t−1}−ϵ∇E$

$w^{t+1}=w^t+V_t$

株価のたとえでいうと、勾配降下法が値動きなら

モメンタムは移動平均線、なめらかに移動する

2.AdaGrad アダグラド

過去の反復計算による観測データの形式の情報を動的に取り入れる。

勾配の緩やかな斜面に対して最適解に近づけることができる。急な斜面は苦手

課題として、学習率が徐々に小さくなるので鞍点(馬の鞍の形)問題を引き起こすことがある。

3.RMSProp

AdaGradの鞍点問題を解消したバージョン

局所的最適解にはならず、大域的最適解になる。

4.Adam アダム　　

モメンタムやRMSPropのメリットをとったいいとこ取りでこの中で最強。

鞍点を抜ける能力が高い。

スムーズな、なだらかな曲線で収束するので学習が進みやすい。Ftrlのような飛び跳ねるような収束の場合、学習が進まないことがある。

参考)

最適化手法ごとの収束の様子のアニメーション

https://github.com/Jaewan-Yun/optimizer-visualization

実装演習

2_4_optimizer.ipynb

＊正答率トレーニング出力部分は長いのでトリムしました。

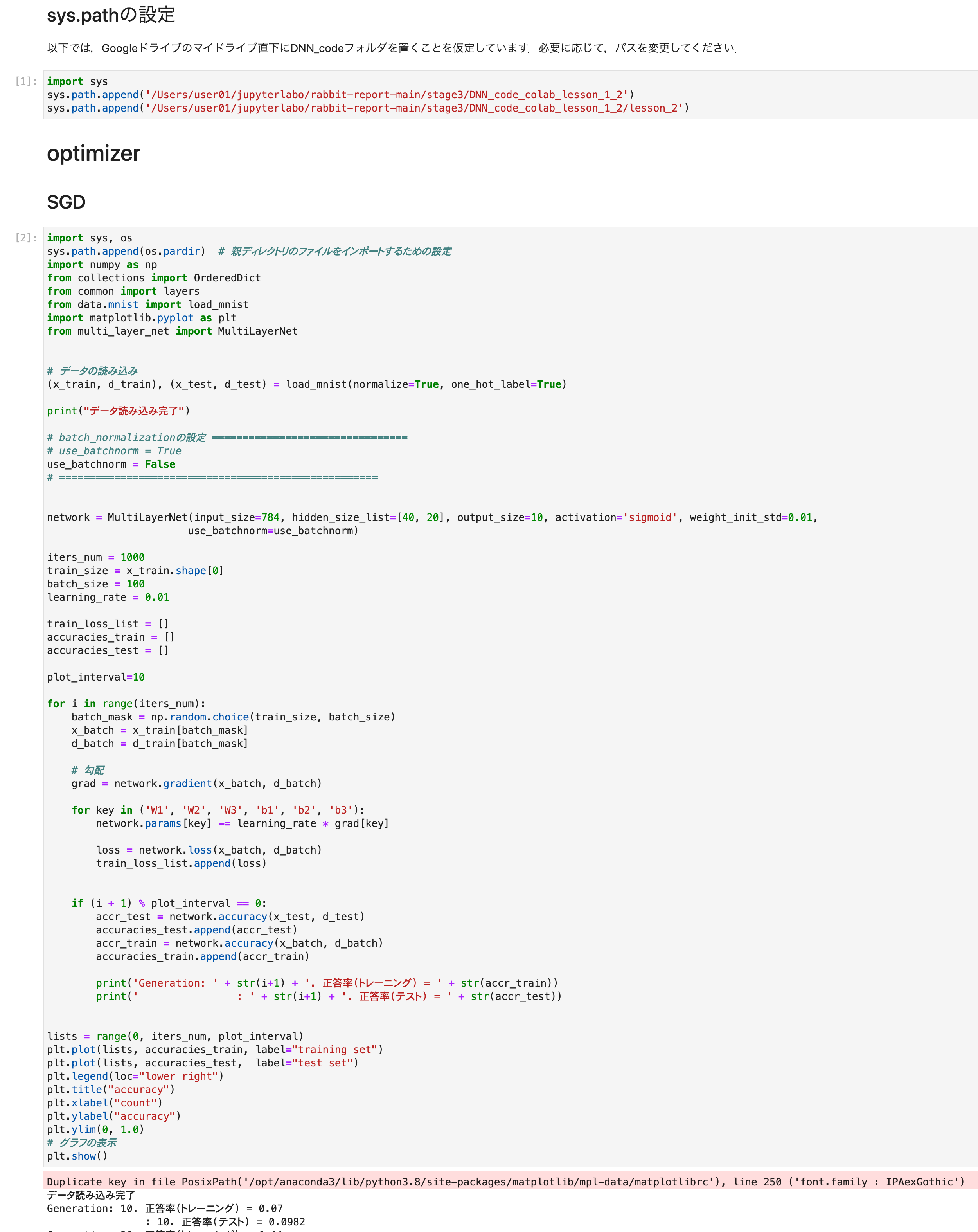
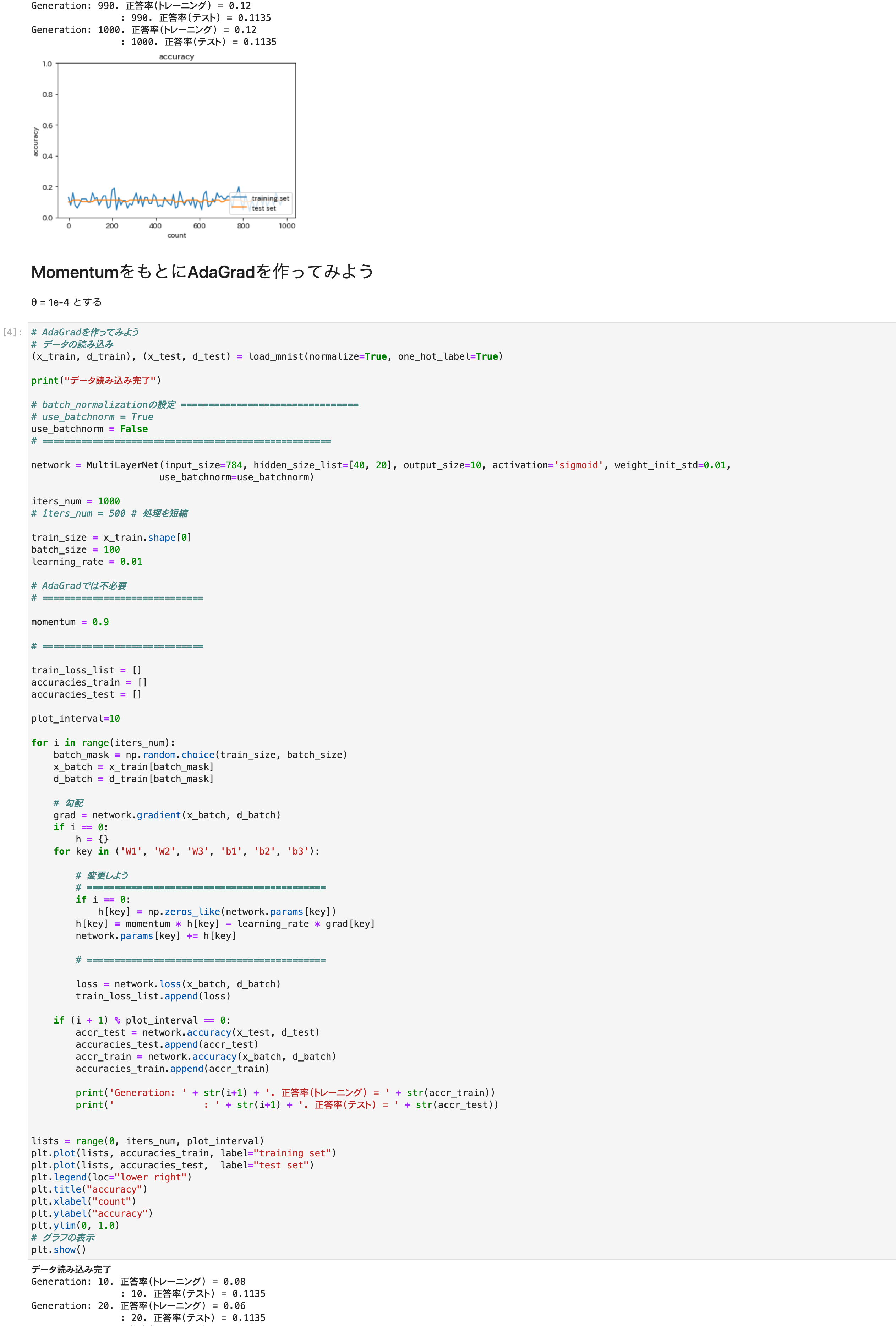
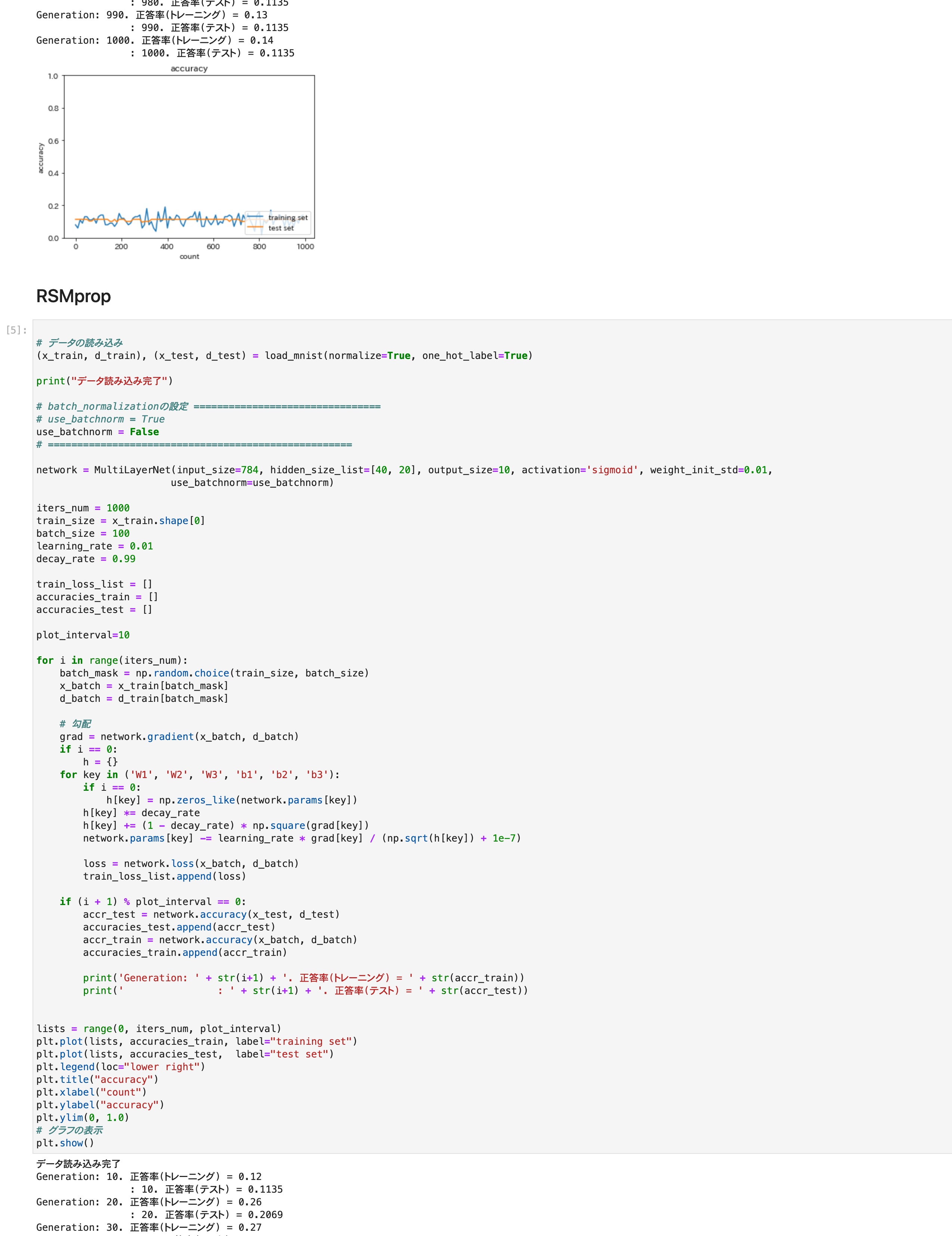
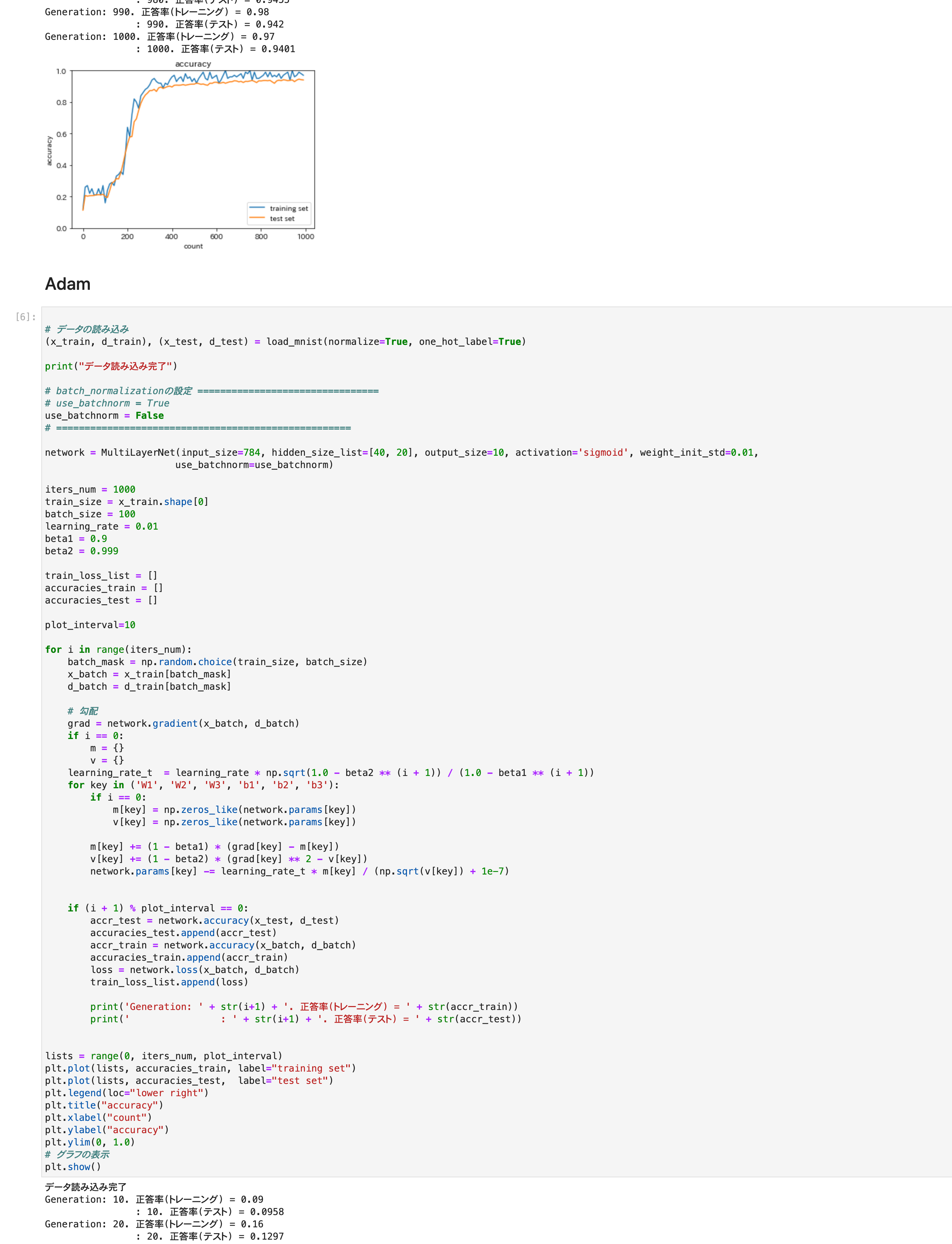
４つの最適化手法を実行。

グラフは正答率

最初の２つ、SGDとアダグラドはうまく学習できなかった

RMSpropとアダムはうまく学習できた